Introducing the Amoeba Sisters Hardy Weinberg Worksheet Answers, an invaluable resource for understanding the fundamentals of population genetics. This comprehensive guide delves into the intricacies of the Hardy-Weinberg principle, providing a thorough analysis of the Amoeba Sisters worksheet and its key concepts.
Through a series of engaging examples and step-by-step solutions, this guide empowers students to master the application of the Hardy-Weinberg principle in real-world scenarios, including the study of genetic disorders and the prediction of evolutionary trajectories.
Hardy-Weinberg Principle: Amoeba Sisters Hardy Weinberg Worksheet Answers
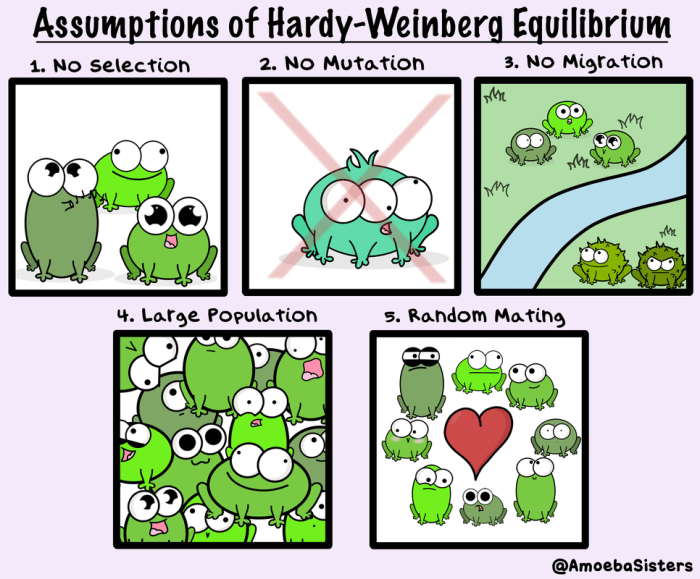
The Hardy-Weinberg principle, also known as the Hardy-Weinberg equilibrium, is a fundamental concept in population genetics that describes the conditions under which the genetic variation in a population will remain constant from one generation to the next. This principle is based on the assumption that there is no selection, mutation, migration, or non-random mating occurring within the population.
The Hardy-Weinberg equilibrium is expressed by the following equation:
“`p^2 + 2pq + q^2 = 1“`
where:
- p is the frequency of the dominant allele
- q is the frequency of the recessive allele
This equation can be used to calculate the expected genotype frequencies in a population. For example, if the frequency of the dominant allele is 0.6 and the frequency of the recessive allele is 0.4, then the expected genotype frequencies would be:
- p^2 = 0.6^2 = 0.36 (homozygous dominant)
- 2pq = 2 – 0.6 – 0.4 = 0.48 (heterozygous)
- q^2 = 0.4^2 = 0.16 (homozygous recessive)
Examples of Hardy-Weinberg Equilibrium in Natural Populations
The Hardy-Weinberg equilibrium has been observed in a variety of natural populations, including:
- Human populations
- Fruit flies
- Bacteria
In these populations, the allele frequencies have remained relatively constant over time, indicating that the Hardy-Weinberg equilibrium is a good approximation of the genetic dynamics of these populations.
Factors that can Disrupt Hardy-Weinberg Equilibrium
There are a number of factors that can disrupt the Hardy-Weinberg equilibrium, including:
- Selection
- Mutation
- Migration
- Non-random mating
When these factors are present, the allele frequencies in a population will change over time, and the population will no longer be in Hardy-Weinberg equilibrium.
Amoeba Sisters Worksheet
The Amoeba Sisters Hardy-Weinberg worksheet is a valuable resource for students who are learning about the Hardy-Weinberg principle. The worksheet provides a step-by-step guide to solving Hardy-Weinberg problems, and it includes a variety of practice problems.
The key concepts covered in the worksheet include:
- The Hardy-Weinberg principle
- The Hardy-Weinberg equation
- How to calculate genotype frequencies
- How to use the Hardy-Weinberg principle to study genetic disorders
The worksheet also includes a number of helpful tips for solving Hardy-Weinberg problems. For example, the worksheet suggests that students start by drawing a Punnett square to visualize the possible genotypes of the offspring.
Step-by-Step Instructions on How to Solve the Problems in the Worksheet, Amoeba sisters hardy weinberg worksheet answers
To solve the problems in the worksheet, follow these steps:
- Read the problem carefully and identify the given information.
- Draw a Punnett square to visualize the possible genotypes of the offspring.
- Use the Hardy-Weinberg equation to calculate the expected genotype frequencies.
- Compare the expected genotype frequencies to the observed genotype frequencies.
- Draw a conclusion based on your findings.
By following these steps, you can solve any Hardy-Weinberg problem.
Applications of Hardy-Weinberg Principle
The Hardy-Weinberg principle has a wide range of applications in population genetics. Some of the most common applications include:
- Studying genetic disorders
- Predicting the evolution of populations
- Estimating the effective population size
Studying Genetic Disorders
The Hardy-Weinberg principle can be used to study genetic disorders by comparing the observed genotype frequencies in a population to the expected genotype frequencies. If the observed genotype frequencies differ significantly from the expected genotype frequencies, then this may be an indication that a genetic disorder is present in the population.
Predicting the Evolution of Populations
The Hardy-Weinberg principle can be used to predict the evolution of populations by tracking the changes in allele frequencies over time. If the allele frequencies are changing, then this indicates that the population is evolving.
Estimating the Effective Population Size
The Hardy-Weinberg principle can be used to estimate the effective population size of a population. The effective population size is the number of individuals in a population that are actually contributing to the gene pool. The effective population size is often smaller than the total population size, and it can be affected by a variety of factors, such as inbreeding and genetic drift.
Extensions of the Hardy-Weinberg Principle
The Hardy-Weinberg principle is a powerful tool for studying population genetics, but it is important to remember that it is only a simplified model. In reality, there are a number of factors that can disrupt the Hardy-Weinberg equilibrium, such as selection, mutation, migration, and non-random mating.
There are a number of extensions of the Hardy-Weinberg principle that can be used to analyze more complex genetic systems. These extensions include:
- The multiple-allele model
- The non-random mating model
- The selection model
The Multiple-Allele Model
The multiple-allele model is an extension of the Hardy-Weinberg principle that allows for more than two alleles at a single gene locus. This model is useful for studying genetic systems with a high degree of genetic diversity, such as the human ABO blood group system.
The Non-Random Mating Model
The non-random mating model is an extension of the Hardy-Weinberg principle that allows for non-random mating within a population. This model is useful for studying genetic systems in which individuals are more likely to mate with individuals who are similar to themselves, such as inbreeding.
The Selection Model
The selection model is an extension of the Hardy-Weinberg principle that allows for selection against certain alleles. This model is useful for studying genetic systems in which certain alleles are more likely to be passed on to the next generation, such as in the case of antibiotic resistance.
These extensions of the Hardy-Weinberg principle are powerful tools for studying population genetics. By using these extensions, researchers can gain a more complete understanding of the genetic dynamics of natural populations.
Answers to Common Questions
What is the Hardy-Weinberg principle?
The Hardy-Weinberg principle describes the conditions under which the frequencies of alleles and genotypes in a population remain constant from generation to generation.
How can the Hardy-Weinberg principle be used to study genetic disorders?
The Hardy-Weinberg principle can be used to identify populations that are not in genetic equilibrium, which may indicate the presence of a genetic disorder.
What are some of the extensions of the Hardy-Weinberg principle?
Extensions of the Hardy-Weinberg principle include the multiple-allele model and the non-random mating model, which allow for the analysis of more complex genetic systems.